A beginner’s guide to interpreting odds ratios, confidence intervals and p-values
Posted on 13th August 2013 by Tim Hicks

Who is it for?
Students of medicine or from the clinical sciences and professions allied to medicine wanting to enhance their understanding of medical literature they will encounter throughout their careers.
What will I learn and how?
How to interpret odds ratios, confidence intervals and p values with a stepwise progressive approach and a’concept check’ question as each new element is introduced.
How long will it take?
Approximately 20 minutes.
What it is not
A statistical textbook reworded or how to calculate any of these statistics.
Contents:
Introduction
Odds ratio
Confidence interval
P value
Bringing it all together – Real world example
Summary
Self test Answers
Introduction
The first steps in learning to understand and appreciate evidence-based medicine are daunting to say the least, especially when confronted with the myriad of statistics in any paper. This short tutorial aims to introduce healthcare students to the interpretation of some of the most commonly used statistics for reporting the results of medical research.
The scenario for this tutorial is centred around the diagram below, which outlines a fictional parallel two arm randomised controlled trial of a new cholesterol lowering medication against a placebo.
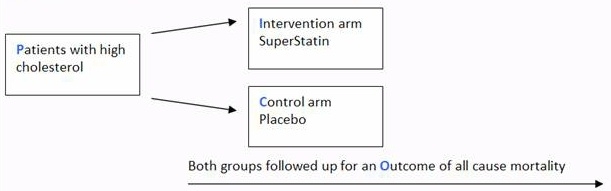
Odds ratio (OR)
An odds ratio is a relative measure of effect, which allows the comparison of the intervention group of a study relative to the comparison or placebo group.
So when researchers calculate an odds ratio they do it like this:
The numerator is the odds in the intervention arm
The denominator is the odds in the control or placebo arm = Odds Ratio (OR)
So if the outcome is the same in both groups the ratio will be 1, which implies there is no difference between the two arms of the study.
However:
If the OR is > 1 the control is better than the intervention.
If the OR is < 1 the intervention is better than the control.
Concept check 1
If the trial comparing SuperStatin to placebo with the outcome of all cause mortality found the following:
Odds of all cause mortality for SuperStatin were 0.4
Odds of all cause mortality for placebo were 0.8
Odds ratio would equal 0.5
So if the trial comparing SuperStatin to placebo stated OR 0.5
What would it mean?
A) The odds of death in the SuperStatin arm are 50% less than in the placebo arm.
B) There is no difference between groups
C) The odds of death in the placebo arm are 50% less than in the SuperStatin arm.
Confidence interval (CI)
The confidence interval indicates the level of uncertainty around the measure of effect (precision of the effect estimate) which in this case is expressed as an OR. Confidence intervals are used because a study recruits only a small sample of the overall population so by having an upper and lower confidence limit we can infer that the true population effect lies between these two points. Most studies report the 95% confidence interval (95%CI).
If the confidence interval crosses 1 (e.g. 95%CI 0.9-1.1) this implies there is no difference between arms of the study.
Concept check 2
So if the trial comparing SuperStatin to placebo stated OR 0.5 95%CI 0.4-0.6
What would it mean?
A) The odds of death in the SuperStatin arm are 50% less than in the placebo arm with the true population effect between 20% and 80%.
B) The odds of death in the SuperStatin arm are 50% less than in the placebo arm with the true population effect between 60% and 40%.
C) The odds of death in the SuperStatin arm are 50% less than in the placebo arm with the true population effect between 60% and up to 10% worse.
P values
P < 0.05 indicates a statistically significant difference between groups. P>0.05 indicates there is not a statistically significant difference between groups.
Concept check 3
So if the trial comparing SuperStatin to placebo stated OR 0.5 95%CI 0.4-0.6 p<0.01
What would it mean?
A) The odds of death in the SuperStatin arm are 50% less than in the placebo arm with the true population effect between 60% and 40%. This result was statistically significant.
B) The odds of death in the SuperStatin arm are 50% less than in the placebo arm with the true population effect between 60% and 40%. This result was not statistically significant.
C) The odds of death in the SuperStatin arm are 50% less than in the placebo arm with the true population effect between 60% and 40%. This result was equivocal.
Bringing it all together – Real world example
A drug company-funded double blind randomised controlled trial evaluated the efficacy of an adenosine receptor antagonist Cangrelor vs Clopidogrel in patients undergoing urgent or elective Percutaneous Coronary Intervention (PCI) who were followed up for specific complications for 48 hrs as outlined in the diagram below (Bhatt et al. 2009).
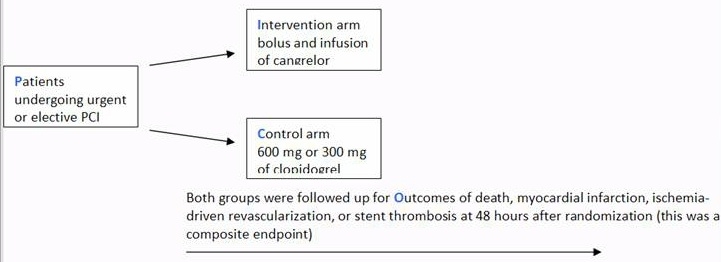
The results section reported “The rate of the primary efficacy end point was … (adjusted odds ratio with Cangrelor, 0.78; 95% confidence interval [CI], 0.66 to 0.93; P=0.005)
What does this mean?
A) The odds of death, myocardial infarction, ischemia-driven revascularization, or stent thrombosis at 48 hours after randomization in the Cangrelor arm were 22% less than in the Clopidogrel arm with the true population effect between 34% and 7%. This result was not statistically significant.
B) The odds of death, myocardial infarction, ischemia-driven revascularization, or stent thrombosis at 48 hours after randomization in the Cangrelor arm were 34% less than in the Clopidogrel arm with the true population effect between 7% and 22%. This result was statistically significant.
C) The odds of death, myocardial infarction, ischemia-driven revascularization, or stent thrombosis at 48 hours after randomization in the Cangrelor arm were 22% less than in the Clopidogrel arm with the true population effect between 34% and 7%. This result was statistically significant.
Summary
This is a very basic introduction to interpreting odds ratios, confidence intervals and p values only and should help healthcare students begin to make sense of published research, which can initially be a daunting prospect. However it should be stressed that any results are only valid if the study was well designed and conducted, which highlights the importance of critical appraisal as a key feature of evidence based medicine.
I do hope you enjoyed working through this and would appreciate any feedback on the content, design and presentational aspects of this tutorial.
Self test Answers
Concept check 1. The correct answer is A.
Concept check 2. The correct answer is B.
Concept check 3. The correct answer is A.
Bringing it all together – Real world example. The correct answer is C.
You may also be interested in these blogs:
Why should students know about kappa value?
Efficacy of drugs: 3 examples to get you to truly understand Number Needed to Treat (NNT)
Key to statistical result interpretation: P-value in plain English
Surrogate endpoints: pitfalls of easier questions
How did they determine diagnostic thresholds: the stories of anemia and diabetes
References:
Bhatt DL, Stone GW, Mahaffey KW, Gibson CM, Steg PG, Hamm CW, Price MJ, Leonardi S, Gallup D, Bramucci E, Radke PW, Widimský P, Tousek F, Tauth J, Spriggs D, McLaurin BT, Angiolillo DJ, Généreux P, Liu T, Prats J, Todd M, Skerjanec S, White HD, Harrington RA. CHAMPION PHOENIX Investigators. (2013). Effect of platelet inhibition with cangrelor during PCI on ischemic events. N Engl J Med. Apr 4;368(14):1303-13.



No Comments on A beginner’s guide to interpreting odds ratios, confidence intervals and p-values
I’m trying to get a better understanding of medical research/literature (and not just read the conclusion without any point of reference) and this helped a lot. I appreciate the practice questions. Thank you!
14th January 2024 at 6:03 pmThat’s really good to hear, Ian, thank you for the comment.
15th January 2024 at 11:44 amI found this a lot more helpful than the videoclip I watched from an exam prep provider.
12th May 2023 at 1:05 pmPlease create more similar contents as the one above.
Thanks.
Thank you! This really helped with my understanding of how the 3 concepts work together to present the data findings.
10th May 2023 at 1:03 pm