The 3 defects of the median
Posted on 27th May 2016 by Tran Quang Hung

You may have heard about them a lot of times: mean and median.
Both of them signify some kind of “average” value.
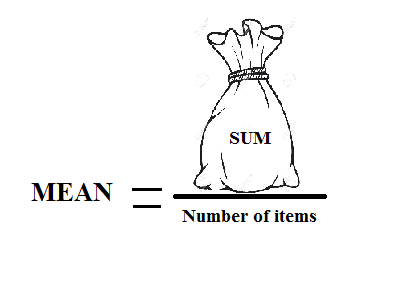
To calculate a mean, you add up all the values and then divide the sum by the number of items on your list.
The median is the half-way point of your list of numbers: half of the sample have values higher than the median and half have values lower than the median.
Median has come to be known for its fair reflection in the case of outliers, or in a population with skewed distribution.
For example, you want to know the average annual outcome of the following population.
 The mean annual income of the population is 135,000 USD. But this salary is higher than that earned by 80% of the population.
The mean annual income of the population is 135,000 USD. But this salary is higher than that earned by 80% of the population.
The median income is 90,000 USD. 50% of the population has lower earnings than this amount, and 50% has higher earnings. So, the median represents the “average” concept in a better way.
However, the median is not an impeccable statistic. There are several things that we should consider when using it for communicating statistical information.
Let me tell you about 3 “sins” of the median.
1/ Median does not convey the information of min and max values
Suppose that the median annual income of Yabada’s citizens is 120,000 USD (you will only find the name Yabada in a wonderland map). What is the highest salary?
You do not know the answer, right?
The highest salary could be 250,000, or 350,000, or even 1M USD. It could be whatever. Simply because, by itself, the median does not provide you with that information.
And even if you know the highest value, you cannot tell the lowest value, either.
You will need more than just a simple median.
2/ Median may lead to a false impression
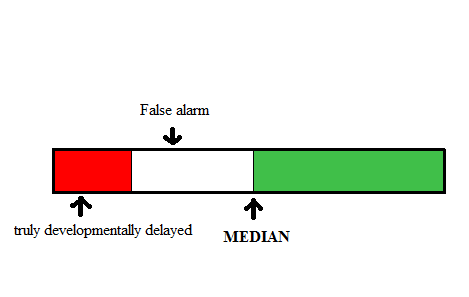
“By the age of 7 months, your son should learn to sit without help.” says a doctor. He is trying to communicate the median concept (that is, the 50th percentile point) to parents.
Unfortunately, parents may not fully understand what the median means. So, when translated into lay language, the doctor may be misinterpreted by parents as saying: “Normally, your son should learn to sit without help at the age of 7 months. If your son cannot sit at 7 months, he is developmentally delayed.”
In this case, 50% of parents could fall into anxiety because their babies are labeled “subnormal”. And the majority of those worries are unnecessary.
So, which data should pediatricians communicate to parents?
Laura Sices wrote an article, in which she proposed 3 figures that doctors should bring into the consultation [1].
The first figure helps to make parents aware of the time when their babies may begin to acquire a given developmental skill. For some skills, infants and young children are at risk of physical injury. For example, parents should know the age at which their babies may start to explore the world by mouth. And parents should hide tiny things that could be dangerous to their offspring before this time. The 10th percentile is chosen for this purpose. (i.e. the point at which 10% of children will have acquired the relevant skill).
The second figure is used to provide information about what is typical at which age. The 50th percentile (that is, the median) is helpful in this case.
The third figure serves as a red flag. If a child is not yet demonstrating an important skill observed in most children that age, the child requires further screening and assessment. The 90th percentile (or another threshold derived from clinical research) is chosen for this purpose. (i.e. the point at which 90% of children will have acquired the skill and thus a ‘reg flag’ would be raised if a child had not acquired the skill by this point).
The median survival time provides another example of where a false impression could be created.
If the median survival time in a given disease is eight months, the chance of surviving at least eight months or longer after starting treatment is 50%. However, in lay language, it is frequently misinterpreted as “I will probably be dead in eight months” [3]. My goodness!
Just keep in mind that 50% patients live longer than that point.
3/ Median is not good for planning
You are planning for a picnic. And you are wondering how many pizzas you should prepare for 10 people.
Let me provide you some info. The mean value: 1 pizza/person/meal. The median value: 1.2 pizza/person/meal.
Which average figure would you choose for planning the meal?
In this case, an arithmetic average (that is the mean value) will work. Remember that mean = sum (the number of pizzas needed) / the number of participants. So, just get the mean value multiplied by 10 people. And you will know that you should prepare 10 pizzas for the trip.
A median cannot tell you about the max, the min, or the total value.
When it comes to planning, mean is better than median.
REFERENCES
1/ Laura Slices. Use of developmental milestones in pediatric residency training and practice: time to rethink the meaning of the mean. J Dev Behav Pediatr. 2007;28(1):47-52.
2/ Darrell Huff. How to lie with statistics. 1954.
3/ Stephen Jay Gould. The median isn’t the message.
All of the images featured in this blog have been created by the blog author.
Read more of Tran’s blogs here:
Efficacy of drugs: 3 examples to get you to truly understand Number Needed to Treat (NNT)
How did they determine diagnostic thresholds: the stories of anemia and diabetes
Key to statistical result interpretation: P-value in plain English
Surrogate endpoints: pitfalls of easier questions
Why should medical students know about kappa value?

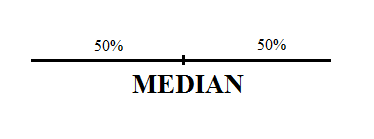



No Comments on The 3 defects of the median
I love this simply explained for a lay person to understand ,very helpful
29th June 2016 at 7:57 amThanks a lot, Rebecca. I’m glad you like it.
29th June 2016 at 9:17 amGreat article, thank you very much. If this is the case, why is median survival often used in cancer stats including by CRUK, in place of mean survival?
30th May 2016 at 12:38 pmNice question, Freya. As I noted in the article above, mean reflects the average value in a better way when the data is skewed. And that’s the case with survival data. Imagine that in a study with 100 cancer patients, 99 die before 5 months, 1 survives 5 years. If we use mean, the average survival time will be > 5 months => longer than the survival time of 99% patients. Median gives us a better estimate.
31st May 2016 at 11:21 am