What are Type I and Type II Errors?

Posted on 21st April 2017 by Priscilla Wittkopf

When conducting a hypothesis test, we could:

• Reject the null hypothesis when there is a genuine effect in the population;
• Fail to reject the null hypothesis when there isn’t a genuine effect in the population.

However, as we are inferring results from samples and using probabilities to do so, we are never working with 100% certainty of the presence or absence of an effect. There are two other possible outcomes of a hypothesis test.

• Reject the null hypothesis when there isn’t a genuine effect – we have a false positive result and this is called Type I error.
• Fail to reject the null hypothesis when there is a genuine effect – we have a false negative result and this is called Type II error.

So in simple terms, a type I error is erroneously detecting an effect that is not present, while a type II error is the failure to detect an effect that is present.

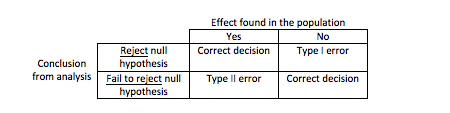
Type I error

This error occurs when we reject the null hypothesis when we should have retained it. That means that we believe we found a genuine effect when in reality there isn’t one. The probability of a type I error occurring is represented by α and as a convention the threshold is set at 0.05 (also known as significance level). When setting a threshold at 0.05 we are accepting that there is a 5% probability of identifying an effect when actually there isn’t one.

Type II error

This error occurs when we fail to reject the null hypothesis. In other words, we believe that there isn’t a genuine effect when actually there is one. The probability of a Type II error is represented as β and this is related to the power of the test (power = 1- β). Cohen (1998) proposed that the maximum accepted probability of a Type II error should be 20% (β = 0.2).

When designing and planning a study the researcher should decide the values of α and β, bearing in mind that inferential statistics involve a balance between Type I and Type II errors. If α is set at a very small value the researcher is more rigorous with the standards of rejection of the null hypothesis. For example, if α = 0.01 the researcher is accepting a probability of 1% of erroneously rejecting the null hypothesis, but there is an increase in the probability of a Type II error.

In summary, we can see on the table the possible outcomes of a hypothesis test:

Have this table in mind when designing, analysing and reading studies, it will help when interpreting findings.

References

COHEN, J. 1990. Things I have learned (so far). American psychologist, 45, 1304.

COHEN, J. 1998. Statistical Power Analysis for the Behavioral Sciences, Lawrence Erlbaum Associates.

FIELD, A. 2013. Discovering statistics using IBM SPSS statistics, Sage.

Tags: