The mean: simply average?
Posted on 22nd October 2014 by Ashline Amilcar

Calculating the mean is easy
The mean is one of the most used methods to summarize data. It is quite easy to calculate: the sum of the values of the entries divided by the count of these entries.
But..
The mean is not located in the data set!
As seen above, the mean is not a value of the data set. When we read that the mean of children per family is 1.86, we immediately think that it’s impossible to have 0.86 children. So even when a list of data contains only entire numbers, their average is not necessarily an entire number.
Above the mean, below the mean….
As a measure of central tendency, the mean is not a point that divides data in two halves, the median does. The amount of values located above or below the mean are not necessarily the same. The mean can be defined as the value that each participant would receive if the sum is divided equally among all members in a group. It is a point where the data’s values are balanced, just like a seesaw.
The extreme values
The mean is affected by extreme values. It’s more obvious when talking about the average of income. For example many countries have a lot of people whose income is low but with a few people earning a lot. The mean of the population income tends to rise for just 1 person who has an extremely high income. In certain cases, the mean might not be the most representative measure of data.
The mean of the mean
When you have more than one mean, be aware of their weights when calculating the mean of them. For example a class divided in three sections of 15, 15, and 30 students. The average of section 1, 2 and 3 is 10, 5, and 20 respectively. What is the average of the class?
The mean is just one way of calculating an average for a given data set. It doesn’t always gives us what we need, and at those times other methods, such as the median or mode, may be more useful.

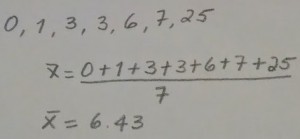
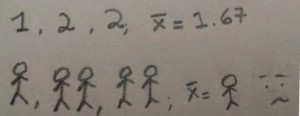
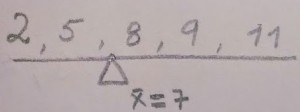
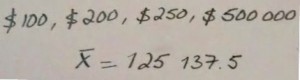



No Comments on The mean: simply average?
Hey,
There’s an error in your last example: the text has the average as: “5, 15, and 20 respectively” but the image is 10, 5 and 20
18th April 2022 at 6:26 amThank you – the text has been updated to reflect the image. Thanks for spotting this.
19th April 2022 at 2:18 pm