Comparison groups should be similar
Posted on 5th September 2017 by Jessica Rohmann

This is the fourteenth blog in a series of 36 blogs based on a list of ‘Key Concepts’ developed by an Informed Health Choices project team. Each blog will explain one Key Concept that we need to understand to be able to assess treatment claims.
In the previous blog in this series, we discussed the need to make fair, reliable comparisons to evaluate the effects of a treatment. But are all comparisons equally fair? In this blog, we will discuss the importance of comparing ‘like with like’, strategies to minimize differences between groups, and how to critically read and evaluate the quality of comparisons made in research reports.
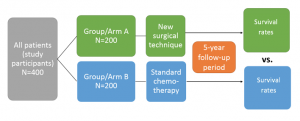
To set the stage, let’s say we want to conduct a study to evaluate whether a new surgical treatment improves overall survival of patients (n=400) with a tumour.
To assess whether our new treatment is better than the current standard treatment (say, chemotherapy), we should create two study groups, by assigning 200 of the participants to group A (treatment arm) and 200 to group B (comparison arm). After five years, we will compare overall survival (see figure 1 below). If the new surgery is more effective than the standard chemotherapy treatment, we would expect to see fewer deaths in group A.
As real life researchers, all we ‘see’ at the end of the study are the trial results (ie. more survivors in group A than B). However, if group A fares better than group B, there are actually three possible scenarios:
(1) our surgical intervention works better (ie. has a stronger positive effect on survival than the standard chemotherapy treatment)
or (2) the difference in prognosis we observe is not due to superiority of the intervention but rather due to pre-existing differences between the people in the groups
or (3) differences are explained by the play of chance.
Now, how do we decide which 200 patients are allocated to each study arm?
Thinking abstractly, we want individuals in group B to reflect the characteristics of the individuals in group A as if they had simultaneously been in group B.
This impossible scenario is known in epidemiology as the ‘counterfactual ideal’ (1). To approximate this in the real world, we must ensure group B is similar on average to group A in any factors that could impact the risk of having the outcome (in this case, death). Some of these factors we may already know and have measured (age, sex, ethnicity, etc.) but others are unknown/unmeasured (genetic predisposition, stress, diet, etc.)
By ensuring our two groups have similar prognoses (comparing ‘like with like’), we can increase our confidence that any difference we see is due to the treatments and not due to patient differences.
Another important component of comparing ‘like with like’ is parallel testing of the groups.
Back to our example: if we had tested our new surgical intervention against a placebo and then attempted to compare its effects to the effects of chemotherapy treatment tested in a different trial years earlier (a so-called historical comparison), we would likely be misled by the results. This is especially problematic if the difference between the two treatment effects is not very large (2). (Although it should be noted that inadequate sample size is important regardless of study design).
Even if the study designs and groups appear similar, differences in external factors between the studies such as the quality of nursing, improved medical developments in the care of comorbidities, as well as differences in unknown, unmeasured factors will likely lead to differences in mortality risk between groups. Therefore, any comparisons made will be unreliable. The bottom line? If groups are not tested at the same time, under the same conditions, there is a good chance they will differ.
So, what technique can we use to allocate participants fairly to comparison groups and ensure an unbiased comparison?
Randomization ensures that both groups have a similar prognosis for the outcome before the start of treatment and that any differences will be chance differences. This thus best approximates the counterfactual ideal, as described above.
Most commonly, participants are assigned to groups using a computer-generated list of random numbers. Other methods include pre-defined treatment schedules and sealed envelopes with group assignments drawn at random. Again, it is very important that this random allocation occurs before the study starts (prospective allocation) to ensure parallel testing. It is also important that the allocation schedule is concealed.
Despite its advantages, there are two major drawbacks to random group allocation
- Randomization can fail, especially with very small sample sizes because the study arms can become out of balance simply due to chance (3). Importantly, this is not a problem with randomization per se, but rather a problem with inadequate sample size.
- Though ideal for testing treatments, for some research questions a randomized controlled trial is inappropriate due to ethical or practical concerns. For example, it would be unethical to randomize individuals to a ‘smoking’ vs. ‘no smoking’ group to test whether smoking causes cancer.
Remember, anyone can claim that their study makes a fair comparison, but unfortunately some research does not ensure truly unbiased, random group allocation.
Imagine if we had assigned our hypothetical study participants to groups based on the numbers of their hospital rooms; allocating patients in lower-numbered rooms (1-10) to group A and patients in higher-numbered rooms (11-20) to group B. This is not random allocation. Can you see why?
- If the severe, high-risk patients are normally situated in low number rooms (closer to the nurses’ station), more severe cases will end up in group A, inflating the risk for the outcome (death) in this group.
- If a doctor is privy to this allocation scheme and believes the surgery is more effective, he may send his sickest patients into one of the lowered numbered rooms instead of a room at random, again increasing the risk in group A.
Allocating participants in this way could create differences in prognosis for the outcome between groups. If the groups differ in baseline risk, we cannot reliably assess the effect of our treatment on outcomes.
When you are reading a study using a ‘randomized’ design, ask yourself, were the patients really allocated to groups at random? Do you see any patterns that leads you to believe certain types of patients were more likely to be allocated to a particular group? Take a look at the baseline characteristics (usually Table 1 of the paper). If you are not convinced the groups are comparable, the results probably do not hold much water, regardless of how tempting it may be to believe them.
The author wishes to thanks Maartje Liefting and Bob Siegerink for helpful feedback on an earlier version of this post.
Learning resources which further explain why comparison groups should be similar
Read the rest of the blogs in the series here
References (pdf)
 Testing Treatments
Testing Treatments
Take home message: