Non-Inferiority Trials: Understanding the Concepts
Posted on 18th March 2022 by Vinay Jaikumar

What will I learn from reading this blog?
- Find out what a non-inferiority trial aims to establish
- Understand the rationale of deriving the non-inferiority margin
- Learn what factors can impact the non-inferiority margin and how to critically appraise non-inferiority studies
This blog deals with slightly complex concepts. While it may seem easier for individuals with basic experience in study designs and other varieties of randomized controlled trials, students with little to no expertise in trial designs might find it complex. While not completely necessary, students can benefit by referring to these S4BE blogs beforehand to enable a better understanding of the concepts and graphical plots in this blog:
- Confidence intervals: A beginner’s guide to interpreting odds ratios, confidence intervals and p-values and Confidence intervals should be reported
- Forest plots: Tutorial: How to read a forest plot and Forest plot at a glance
- Heterogeneity: Heterogeneity: what is it and why does it matter?
What is a non-inferiority trial?
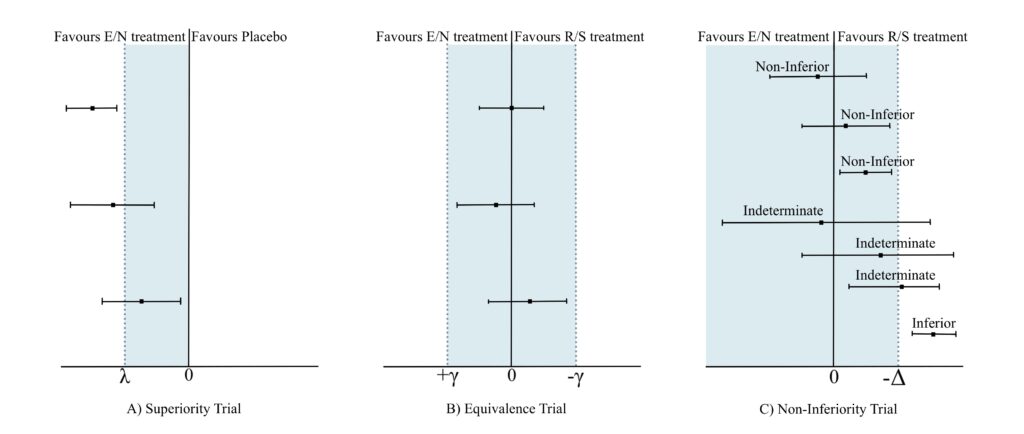
The prototypical randomized clinical trial is a superiority trial. This primarily aims to ascertain whether an experimental/novel (E/N) treatment strategy is superior to the established reference/standard (R/S) or placebo strategy in improving health/functionality outcomes or mitigating morbidity or mortality outcomes (Figure 1A).
Targeted at improving current healthcare practices, newer medications and devices can offer improved benefits. These may include availability, efficacy, cost, dosage/dosing schedule/route of administration/tolerability, side effect profile, reduced length of hospital stays, lower frequency and length of clinical follow up, reduced long term disability, and improved quality of life. Even considering these benefits, comparing an E/N against a placebo would be considered unethical in the treatment of a medical condition which has an established and/or efficacious R/S strategy, against which the comparison should have been originally sought. During this venture, establishing superiority of E/N against R/S is desirable for the researchers. However, under circumstances when inferences about superiority cannot be demonstrated, the next best strategy would be to assess if the E/N treatment is equivalent to, or at the minimum ‘not unacceptably worse’, than the R/S treatment. This introduces us to the concepts of ‘Equivalence Trial’ and ‘Non-Inferiority’ Trial respectively (Figure 1B and 1C). (1-5)
Figure 1
The goal of an equivalence trial is to demonstrate that E/N strategies are equivalent to R/S strategies by employing a margin (shown as γ in Figure 1B) on either side of zero which depicts the maximum tolerable difference for equivalence. If the computed confidence interval of E/N efficacy outcome derived at the end of the trial lies strictly within -γ and + γ, the E/N strategy is said to be equivalent to R/S (Figure 1B). (2,3)
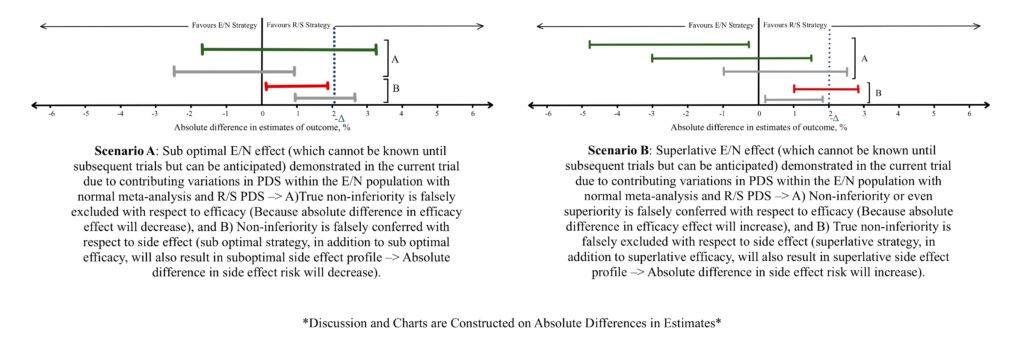
Contrastingly, in non-inferiority trials, while the E/N strategy is definitely not better than the R/S, it is not unacceptably worse (i.e. non-inferior) if the lower limit of the computed 95% CI around the difference between E/N and R/S does not extend beyond a pre-defined margin (shown as -Δ in Figure 1C), also known as the non-inferiority margin. (1-5)
Presenting this as a clinical scenario, let’s suppose an E/N strategy offers additional benefits – such as reduced cost and no hospitalization – compared to the R/S strategy, but there is a loss in efficacy and/or an increased frequency/intensity of side effects. The threshold of ‘not unacceptably worse’ denotes how much loss in efficacy and/or how much increase in frequency/intensity of side effects the patient is willing to tolerate or accept in exchange for the additional benefits. The process so far involves selecting a non-inferiority margin and conducting the trial comparing E/N against R/S. Subsequently calculating the effect outcomes yields the lower bounds of the 95% CI around the effect and if this lies above the -Δ margin, non-inferiority is confirmed, and the trial is deemed a success. If the lower bound of the 95% CI lies above the null threshold and the -Δ margin, then E/N is not only non-inferior but also superior to R/S and the placebo as well. If the upper bound always remains above the -Δ margin, but the lower bound of the 95% CI falls below the -Δ margin, then the effect of E/N is said to be indeterminate. If both the upper and lower bounds are confined below the -Δ margin, the effect of E/N is deemed to be inferior to R/S (Figure 1). (2,3,5)
How do I choose the non-inferiority margin?
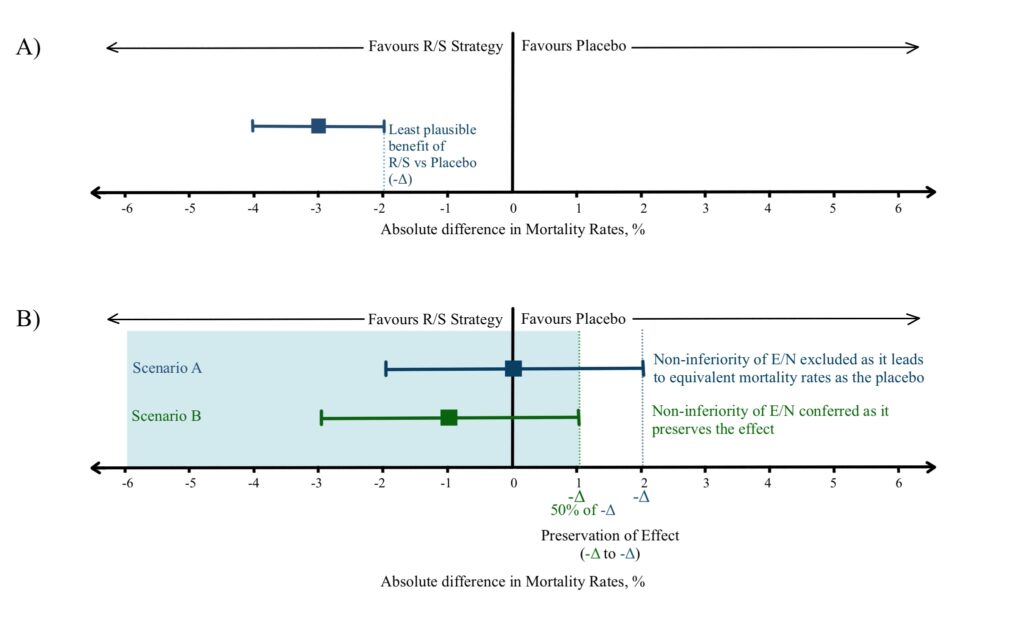
An important step in designing a non-inferiority trial is deriving the non-inferiority margin Δ. This is achieved through a combination of statistical analysis and clinical judgement. (1,3) The FDA Guidance draft provides a widely endorsed strategy where either a single placebo-controlled trial of the R/S strategy or a random-effects meta-analysis encompassing comparable trials supplies the 95% CI around the estimated outcome difference between the R/S and placebo. (6) The process of the FDA strategy is to derive the smallest plausible benefit offered by the R/S strategy i.e., the lower limit of the 95% CI or the limit of the CI closest to no effect (Figure 2). (5) While the lower bound of the 95% CI can serve as the non-inferiority margin -Δ, several considerations must be taken into account which can influence this decision and compels to make additional modifications. (6)
1. Preservation of effect
Let us assume a R/S treatment reduces the mortality rate in a medical condition to 4% compared to 7% in the placebo-controlled group, giving an absolute risk reduction of 3% with 95% CI ranging from 2%-4%. This implies that 2% reduction in absolute risk is the smallest plausible benefit offered by R/S treatment which can be utilized as the -Δ (Figure 2A). (5)
Suppose a less efficacious E/N strategy offering additional benefits is compared with the R/S in a non-inferiority trial. E/N demonstrates a 2% increase in absolute risk of mortality (Point estimate of 0% reduction in mortality with an upper limit of 2% reduction in mortality; Figure 2B, Scenario A). The 2% increase in absolute risk by E/N over R/S nullifies the smallest plausible 2% reduction in mortality benefit by R/S over placebo. This constitutes a likely scenario where the E/N is equivalent to the placebo. Any further increase in E/N absolute risk will imply that the strategy is indeed worse than placebo as well.
This emphasizes the need to preserve the effect conferred by the R/S strategy across all probable scenarios, which has been suggested as a fraction (f) of 50% of the observed smallest plausible benefit by drug regulatory authorities, and this constitutes the new -Δ. In this case, 1% (50% of 2% reduction in absolute risk of mortality by R/S) will be the accepted -Δ and an E/N will be tolerated/accepted (considered non-inferior) if it causes no more than 1% increase in mortality (Figure 2B, Scenario B). The value of fraction f chosen above to derive the -Δ is subject to clinical judgement and patient preference. (5,7,8)
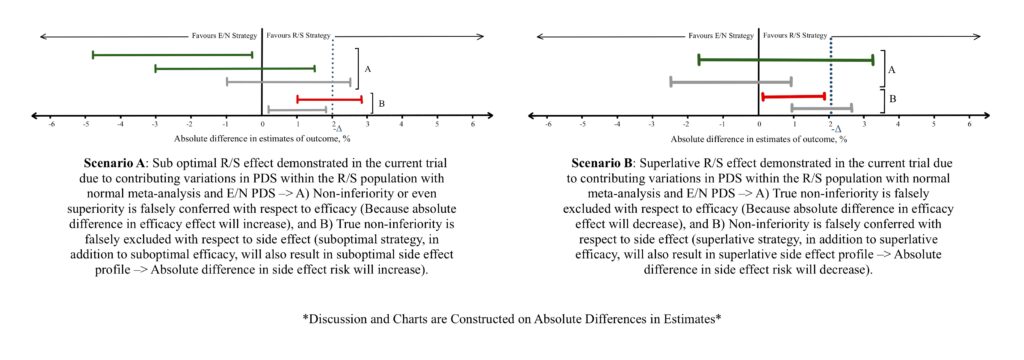
Whilst the above scenario dealt with a loss in efficacy, let us consider a new scenario where a trial compares E/N strategies A and B against a R/S. All of them target the same medical condition, have a similar smallest plausible mortality reduction of 4%, and offer the same additional benefits, but demonstrate different side effect profiles. Let us assume A and B demonstrate an increase in their maximum risks of lethal hemorrhage and non-lethal hemorrhage respectively when compared individually against R/S.
If we choose the traditional f of 50%, patients treated in the drug A comparison (and even physicians) might not be willing to accept a 2% (50% of the smallest plausible 4% benefit) increase in absolute risk of lethal hemorrhage even with additional benefits. They might prefer a smaller acceptable risk, and in extension, want to set a smaller f (for example 30%) to conclude non-inferiority with E/N strategies causing similar lethal side effects. Contrastingly, a higher f (for example 70%) can be chosen for less severe side effects like non-lethal hemorrhage, thus allowing for acceptance of a higher risk of non-severe side effect in exchange for additional benefits.
2. Assay Sensitivity
The superiority of R/S that is established over placebo must be undeniable, reliable, and consistent. The R/S strategy should demonstrate an archetypical established effectiveness outcome within a large responsive population using the appropriate dosage/dosing frequency/route of administration compared to the placebo. Following the above, if the smallest plausible benefit by the R/S strategy is large (a large effect is observed), the f /-Δ chosen must be much smaller than 50% to prevent a false attribution of non-inferiority in E/N vs R/S trials. Under circumstances where an underestimate of the effect size is demonstrated, due to the various factors discussed in the subsequent section, a higher f /-Δ can be chosen to compensate for the underestimated effect size. However, this fraction must be arrived at after a comprehensive scientific and clinical discussion. (7-9)
3. Study Constancy
Performing meta-analyses combines data from a wide group of studies to calculate an effect estimate of the R/S strategy. We need to include studies in the meta-analysis which have the same PDS as the current study:
a) Patient and population characteristics (P)
b) Drug dose/dosing schedule/route of administration/simultaneous additional medication (D)
c) Study design and analysis (S)
Since it is arduous and at times futile to find such a group of homogeneous trials, the heterogeneity in effect sizes must be accounted for which can be accomplished with a random-effects model. However, one should stay aware while using random-effects models which tend to overemphasize the importance of small studies (single centers, more likely to be subject to bias, and less likely to employ quality data and/or efficient analysis methods). This can end in skewed results (10) and is discussed further in the subsequent section. (7-9)
What considerations should be taken into account while choosing the non-inferiority margin?
1. Patient/Population Characteristics
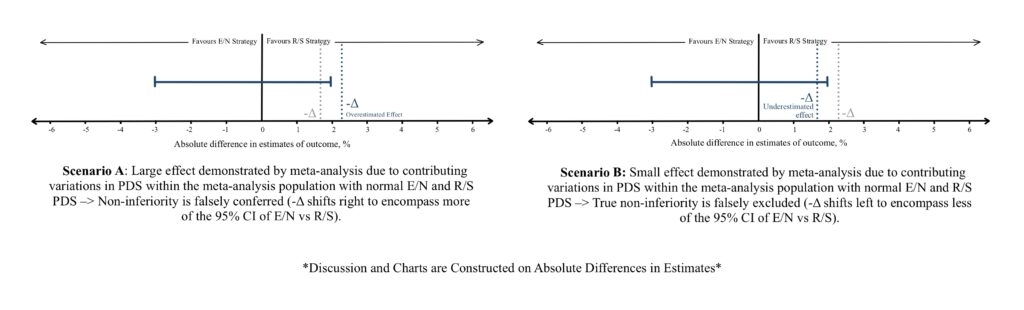
a) Drug resistance such as antibiotic resistance, hyper metabolizers of a drug, or using a simultaneous enzyme inducer leads to a small effect estimate of the drug. Considerations must be taken in establishing the -Δ during the meta-analysis considering such scenarios (Figure 3B), or while evaluating the effect estimates between E/N and R/S (Figure 4A, Figure 5A). Vice versa can be observed if the patient population are hypo metabolizers, liver/renal failure showing increased drug concentrations, or a simultaneous enzyme inhibiting drug is utilized (Figure 3A, Figure 4B, Figure 5B) leads to a larger effect.
b) Disease severity: Milder disease can be met with more effective or acceptable outcomes and can show a large effectiveness estimate compared to severe disease (Figure 3A, Figure 4B, Figure 5B).
c) If patient/population are expected to be non-adherent to a treatment regimen (old age, living alone, dementia, mentally challenged, complex therapeutic schedules, frequent follow ups), a sub optimal effect is seen (Figure 3B, Figure 4A, Figure 5A).
2. Drug/Strategy Characteristics
Suboptimal effect (Figure 3B, Figure 4A, Figure 5A) estimate can be caused by:
a) Different chemical composition of the drug or different procedure
b) Suboptimal dose
c) Lower dosage frequency
d) Suboptimal route of administration (for example orally rather than intravenously)
e) Simultaneous ancillary treatments
f) Setting early effectiveness estimation milestones/follow ups when the drug has not had time to fully manifest its effects
Vice versa can lead to superlative effect estimates (Figure 3A, Figure 4B, Figure 5B).
3. Study characteristics / Study design
a) Reducing the risk of bias through adequate allocation concealment and randomization of patients and prognostic factors, blinding patients, clinicians, and outcome assessors, and allowing complete follow-up yields an unbiased estimate of effect. A failure to achieve this can result in overestimated or underestimated effects.
b) An Intention-to-treat (ITT) or as-randomized analysis preserves the benefits of randomization which is highly desirable for the study. However, considering a scenario where patients do not adhere to the treatment strategy or a study group suffers high rate of attrition, a substantial underestimate of beneficial effect or adverse effect can be demonstrated. Studies chosen for the meta-analysis are predominantly superiority trials which employ an ITT analysis for the most accurate effect estimates. The tendency of these above-discussed PDS factors to skew the final 95% CI must be considered (Figure 3B). Within the current trial comparing E/N and R/S, non-adherence, and attrition result in similar underestimates of effect (Figure 4A, Figure 5A) and should be taken into consideration while interpreting non-inferiority trials.
On the contrary, performing a per-protocol (PP) introduces prognostic imbalances and mitigates the benefits achieved by randomization, but it is more suited for analysis in non-inferiority trials. Since the analysis takes into consideration only those who adhere to the treatment and the study, an over estimation of effect (both efficacy and adverse effect) can be anticipated. Like ITT, PP analysis within included studies can impact the meta-analysis estimate and 95% CI (Figure 3A). When the current trial study groups utilize the PP analysis, an overestimate of effect and 95% CI (Figure 4B, Figure 5B) should considered.
So how do you choose between ITT and PP analysis in deciding the non-inferiority of an E/N strategy ? The FDA guidance offers a straightforward approach. One carries out both ITT and PP analysis. If both demonstrate a consistent result (non-inferior or not non-inferior), the results of the trial can be accepted. When the ITT and PP analysis results straddle the -Δ, (13) the inference of noninferiority is weakened. This further compels to reassess and reconsider the chosen -Δ subsequently at the clinical level.
Clinical considerations in approaching a non-inferiority trial
The first task in implementing a non-inferiority trial result into clinical practice would be to assess the validity of the effectiveness outcomes of the trial. This can be achieved through comprehensive examination of the various contributing factors discussed above. Once the validity is established or the nuances are accounted for, the following step is to assess if the results of the trial can be extrapolated to the clinician/institutional patient population and treatment administration protocol. If a direct extrapolation cannot be made, given the discussion above, one can anticipate the probable range and shift in direction of effectiveness outcomes that can be expected with the current patient population and the treatment administration protocol.
Another critical factor to consider is the patient’s choice with the drug, additional benefits, and -Δ margin. The cumulative decision by the patient and the clinician/institution can form a strong foundation to choose their own non-inferiority margin instead of the ones suggested by the trial sponsor or investigator. This newly accepted -Δ margin in addition to either the original 95% CI or the estimate calculated/adjusted 95% CI for the current population, can modify the decisions of non-inferiority put forth by the trial i.e. shift from a decision of non-inferior to indeterminate/inferior or vice versa. This presents non-inferiority trials not as an absolute principle but more a modifiable guidance that can aid the clinician in improving the healthcare a patient receives. (1-9)