Cluster Randomized Trials: Concepts
Posted on 28th March 2022 by Vinay Jaikumar
What is Cluster Randomization ?
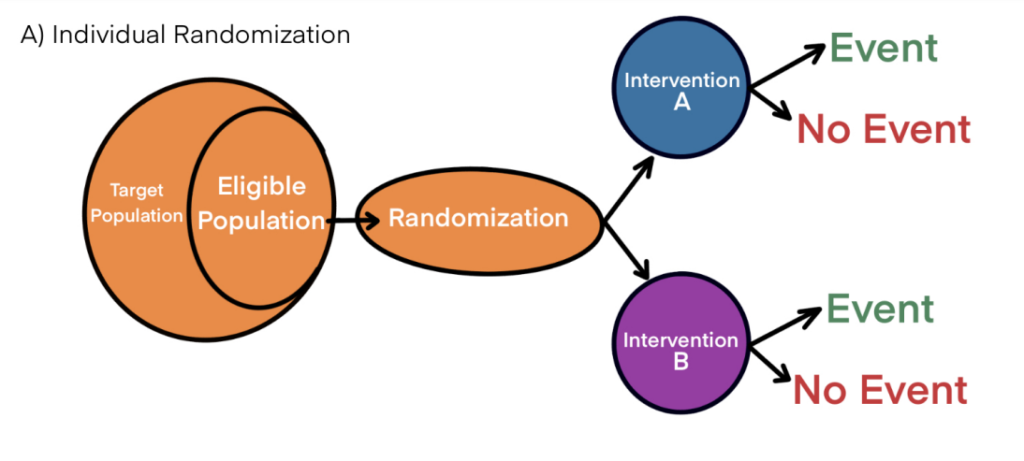
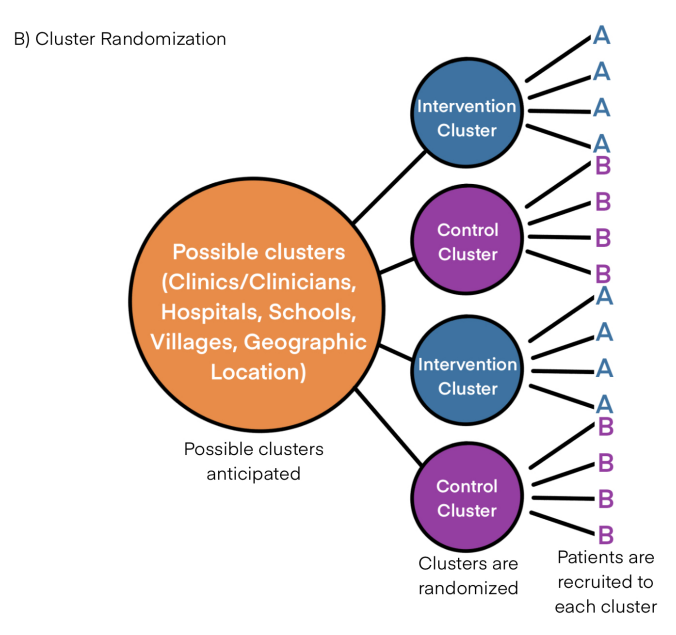
Participants in most clinical trials are randomized to the treatment arms as individuals. However, under circumstances when individual randomization cannot be accomplished (e.g. practical challenges) or isn’t desirable (e.g. contamination), participants are instead randomized as ‘groups of individuals’ or clusters (Figure 1). In a cluster randomization, groups of participants such as within clinical practices, schools, hospital/ICU wards, or regional/geographical areas, serve as the unit of randomization. Cluster randomization is particularly suited for implementation studies like population lifestyle interventions, treatment guideline outcomes, and community vaccinations. (1-3)
But why should we go for cluster randomization ?
1) Practical feasibility of cluster randomization:
Some interventions may be feasible only though the cluster randomization approach. (1-3) For example, let us consider the Salt Substitution and Stroke Study (SSaSS) conducted in Chinese villages. This large scale, open labelled, cluster randomized trial involved 600 villages in China with 21,000 participants (35 participants per village). (4) Participants either had a history of stroke, ≥60 years, or had high blood pressure. The impact of salt substitution (75% : 25% = Sodium Chloride : Potassium Chloride versus Sodium Chloride only) on subsequent strokes, cardiovascular events, and death were studied. The design of cluster trials necessitates such a high sample size. If we were to consider individual randomization within each village, contemplate the logistical requirements of implementing the consent procedures, randomization, and both the treatment interventions in each of the 600 villages. It would be more feasible and efficient if each village/cluster was randomized to the intervention and control.
2) Contamination in cluster randomization:
Contamination is a scenario where the control arm receives the intervention from the participants in the intervention arm or other means. (2,3,5) This tends to dilute the effect of the intervention when compared to controls leading to a Type II error.
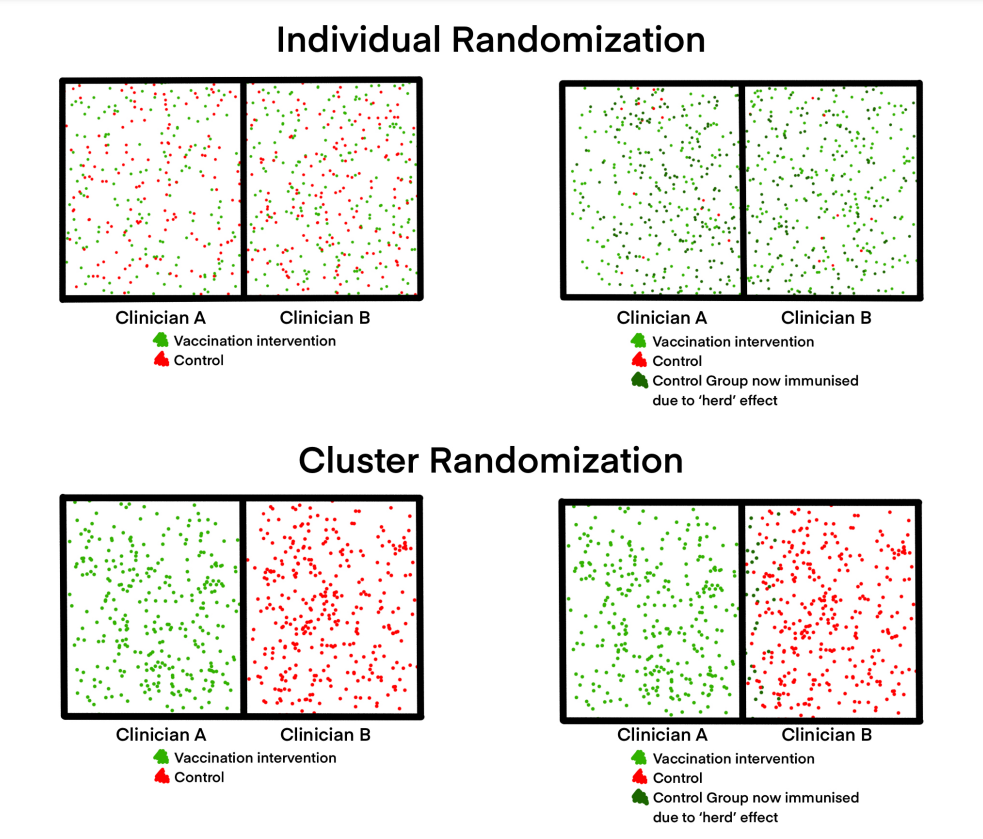
For example, let us consider a vaccine trial in a population for a communicable disease where the vaccine is capable of inducing ‘herd’ immunity. If participants are randomized individually, owing to ‘herd’ effect, the controls will demonstrate an increased resistance to the disease comparable to the intervention group. This underestimates or dilutes the beneficial impact the vaccine provides over the control (Figure 2A). Here, let us utilize a cluster randomization approach. If we cluster participants regionally/according to their locality and randomize them to two clinicians, one designated to administer the vaccine and the other as a control, the possibility of ‘herd’ immunity to take effect will be reduced (Figure 2B).
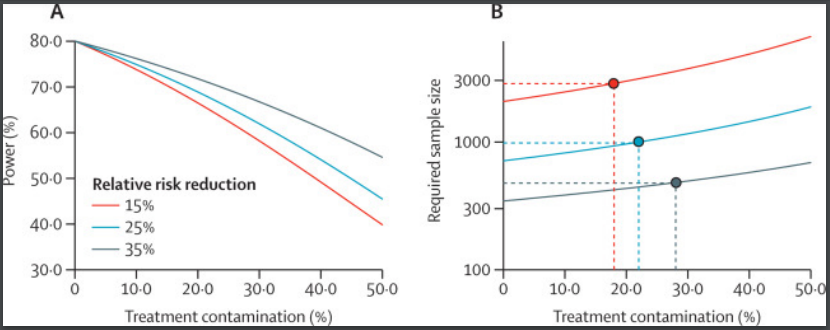
Similarly, trials employing an educational intervention to improve lifestyle of participants at high risk of a disease might randomize participants as clusters to avoid an increased possibility of the intervention group telling the control group about the treatment. Increasing percentage of contamination decreases the power of the study and requires an increased sample size to maintain the power (Figure 3). (2)
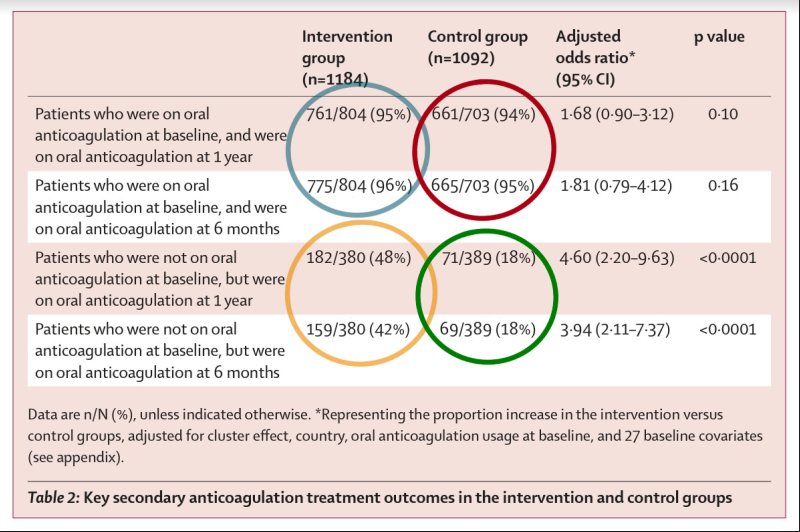
However, while clustering can mitigate the impact of contamination, it is not completely safe from it. Large amounts of contamination can overpower the capacity of clustering to mitigate them. For example, let us consider the IMPACT-AF trial. (6) They explored the role of continuing educational programs, and regular monitoring and feedback in promoting adherence to anticoagulants between two groups of randomized populations with atrial fibrillation.
The first group (Figure 4, blue and red) had already received baseline educational intervention from experienced treating centers and the second group did not (Figure 4, yellow and green). The second group, which hadn’t received baseline education, showed increased proportion of clusters adhering to the anticoagulant at the 6 and 12 month follow up following the intervention (Figure 4, yellow) and the control did not (Figure 4, green). The first group however showed similar rates of adherence between intervention (Figure 4, blue) and control (Figure 4, red) clusters at the 6 and 12 month follow up. This is explicable considering the control arm (Figure 4, red) of the first group received the same educational intervention or contamination initially from the experienced institution.
This forms a plausible explanation for not observing a loss in adherence following the absence of continuing education in the control cluster of the first group. This diluted or underestimated the impact of educational interventions in improving/maintaining the adherence rates between intervention and control clusters. However, reading between the lines, this study conveyed that baseline educational interventions will suffice in maintaining excellent adherence rates to treatment even in the absence of continuing educational intervention. (6)
3) Consent in cluster randomization:
With trials employing individual randomization, consent usually precedes the randomization process. (1,2) In cluster trials, the clusters are initially randomized and designated the intervention or control arm following which participants are assigned to each arm. Individual consent can oftentimes be waived in cluster trials. (1,2) In such scenarios only the consent of the cluster representative (clinician, hospital, school headmaster, village head) will suffice. However, when circumstances do necessitate the informed consent process, an important consideration comes into play. Some refusal of treatment or data collection has been observed in individually randomized trials when acquiring consent follows the randomization process rather than preceding it. (3,7,8) This, in cluster trials as well, will introduce a selection bias. Identifying and informing all participants within potential clusters prior to cluster allocation about all possible intervention alternatives, followed by asking for their consent to participate, can circumvent this hurdle.
Challenges Associated with Cluster Randomized Trials
1) Calculating the sample size:
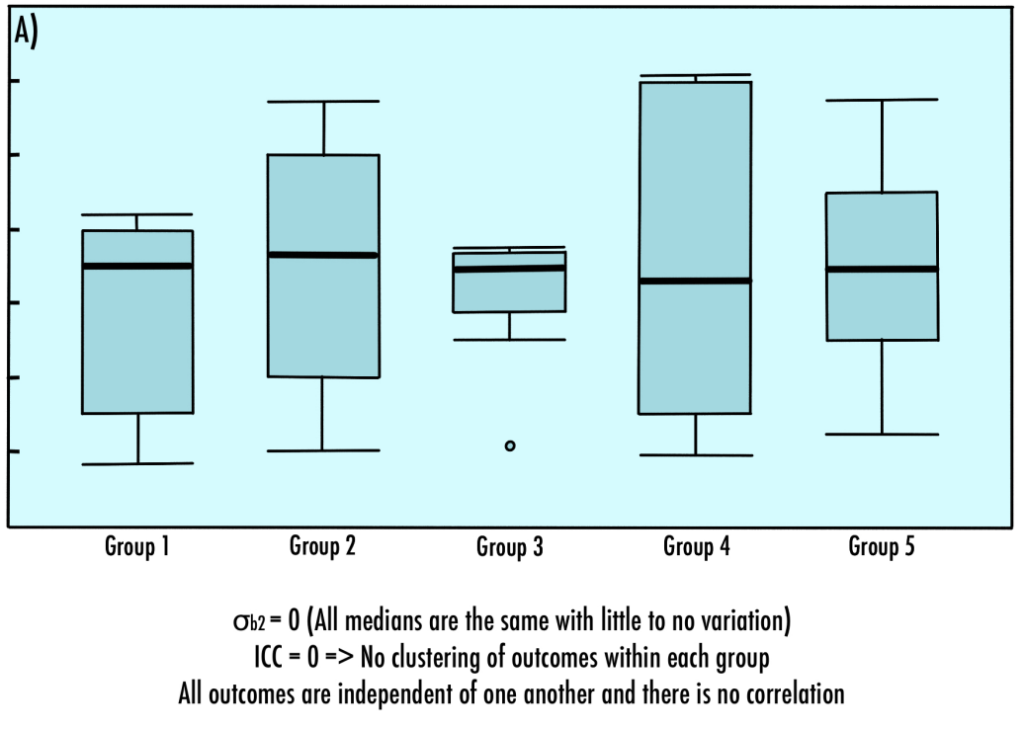
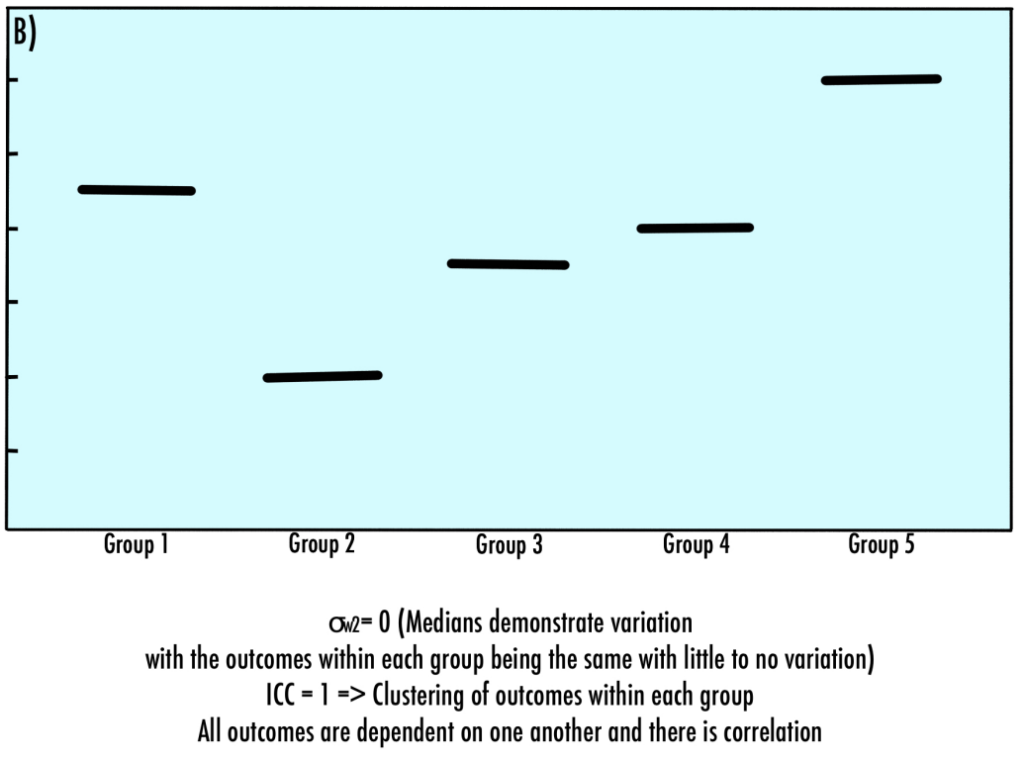
Compared to trials employing individual randomization to test a hypothesis, cluster randomization trials require a significantly larger sample size to test the same. This is because the outcome measurements from participants within a cluster tend to be more alike when compared to those among other clusters. This signifies those observations are not independent and that they are correlated in a cluster randomization compared to individual randomization where observations are assumed to be uncorrelated during sample size calculations. Variance measures the correlation between outcomes. It depicts how distant the observations are spread across from the mean. A variance can never be negative. A variance of zero implies that all observations are the same with no spread on either side of the mean.
The sample size estimation for cluster randomization must consider the variance within clusters (σw2) themselves as well as variance between different clusters (σb2). The Intracluster (Intraclass) Correlation Coefficient (ICC) quantifies the proportion of the total variance (σw2 + σb2) of the outcome variable that is accounted for by the between/inter cluster variance (σb2) and is designated by the symbol rho (ρ).1,2 The variances are derived from previous studies. It should also be noted that variations of ICC are utilized to quantify interrater agreeability where measured/recorded values are compared to see if they are analogous between raters.
ICC (ρ) = σb2 / σw2 + σb2
If the σw2 is zero, that is outcomes within a cluster are the same with little to no variation, the ρ is one (Figure 5B). Accordingly, if the σb2 is zero, that is the outcome between clusters is the same with little to no variation, the ρ is zero as well (Figure 5A).
The ρ finds utility in calculating the design effect. It depicts the inflation factor by which the sample size must be increased in order to maintain the power of the cluster randomized trial. (1,2) The design effect is calculated by:
deff = 1 + (m – 1) ρ
where m is the cluster size and ρ is the ICC. Now the total sample size (N) required to conduct a cluster randomized trial is:
N = n (deff) or N = n (1 + (m – 1) ρ)
where n is the sample size required if we were to undertake individual randomization. N is the total sample size which requires an inflation of deff times of n. (1,2) If cluster size is 1 (m=1) or the ρ is zero (no variation between clusters/clusters are the same/ σb2 is zero), deff is 1 and the sample size for cluster trial is the same as an individually randomized trial. If the ρ is one (no variation within a cluster/observations within a cluster are the same/ σw2 is zero), the sample size required for the cluster trial is multiplied by a factor ρ. Hence, if a greater correlation is observed among participants within a cluster, a greater ρ is obtained. This leads to a larger sample size which will now suffice for accurate effect estimates. (1,2)
The higher the ρ, the larger the sample size, and the difference can be significant. Let us consider an m of 30. The inflation in sample sizes for progressively increasing ρ of 0.001, 0.01, and 0.1 will be by a factor of 1.029, 1.249, and 3.49 respectively.
2) Clustering Effects:
In a clustered environment, participant outcomes have a tendency to be correlated which can be attributable to a common factor. In simpler terms, participants within a cluster will tend to have similar outcomes. For example, patient factors such as age, ethnicity, gender, geographic location, or insurance plans can influence their recruitment under certain clinicians and hospitals. Cluster-level attributes such as the rates of clinicians’ compliance with established clinical decisions for trial will ensure that all participants under that clinician will receive the exact same treatment. Thus, the participants within a cluster will display more similar outcomes compared to other clusters. In addition, participants within a cluster can influence each other through similar attitudes and behaviors resulting in similar rates of compliance with treatment or follow up, and outcomes. Clustering not only impacts cluster trials but individually randomized trials as well. (1,2,9)
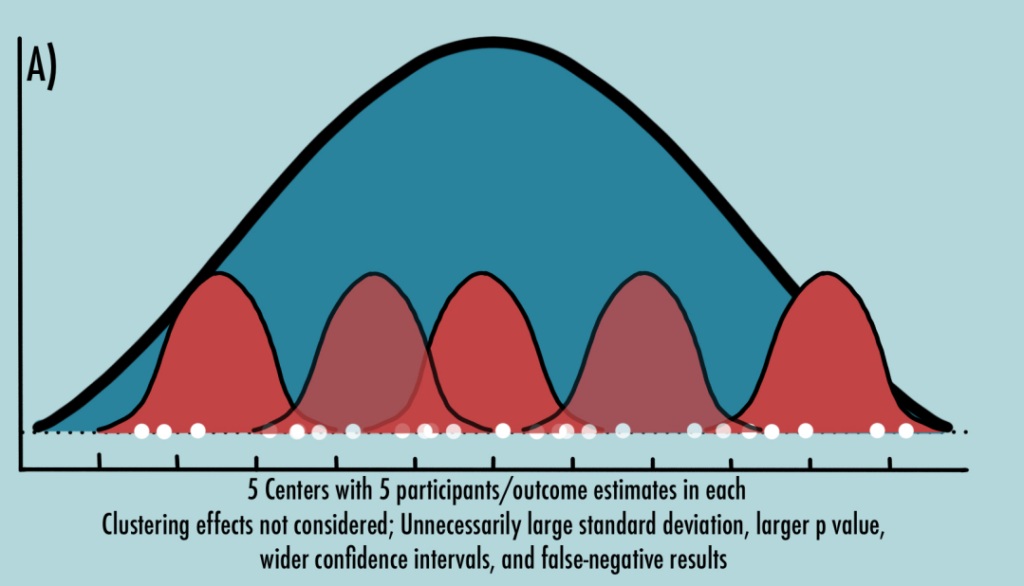
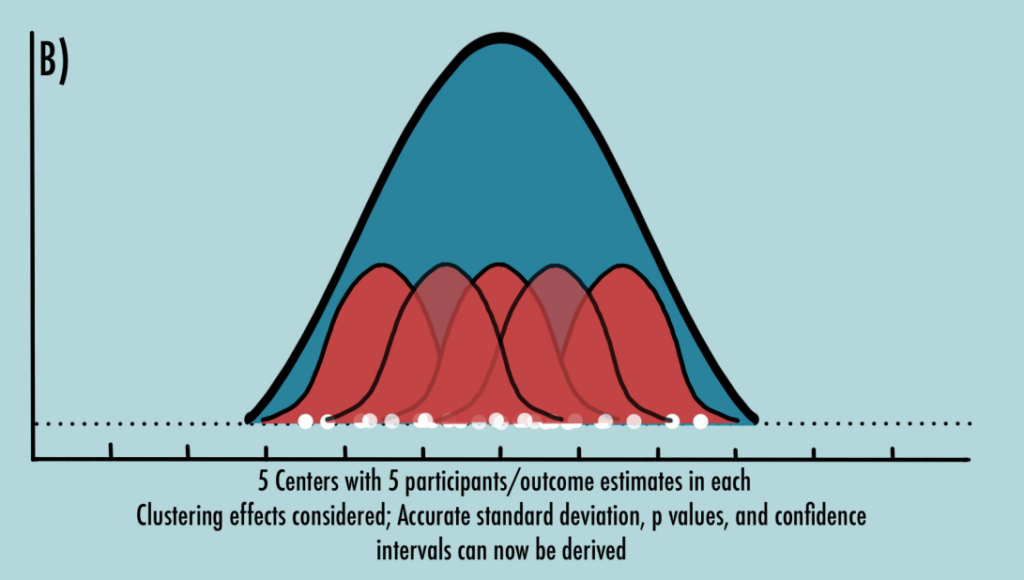
Let us consider an individually randomized study where different centers (For example, geographically separated) are chosen (Figure 6). The participants within each center will include both intervention and control participants. Participants within each center will tend to display similar outcomes with little to no variability (Figure 6, red curves) when compared with participants from a different center. Now, let us pool all intervention participant outcomes across all centers and compare them with pooled control participant outcomes. If clustering is not taken into consideration, while the variation in outcomes can be small within the center, it will be relatively much larger between centers giving rise to unnecessarily larger standard deviations, larger p values, wider confidence intervals, and false-negative results (Figure 6A). Considering clustering mitigates that correlation of outcomes and results in accurate outcome estimates (Figure 6B). (1,2,9)
In cluster trials, this effect is amplified as clusters have either intervention participants or control participants but not both. If the intervention cluster outcomes show a strong positive/negative correlation, if the impact of clustering is not considered, this can even lead to false-positive or false-negative outcomes respectively with inappropriately small p values and narrow confidence intervals. Analysis that considers clustering effects will accurately calculate the variance of outcome estimates. (1,2,9)
3) Selection Bias:
Selection bias in cluster trials can be introduced at the cluster level and at the participant level. (1-3, 9) The initial randomization of clusters is a crucial step and is prone to biased allocation. If clusters are allocated based on predictable outcomes of the yet unrecruited participant population, this introduces selection bias. (1-3, 9) At the individual level, if a participant has characteristics that will predict an outcome despite the intervention or control, one can selectively place the participant into either of the clusters depending on what outcome they want to see. For example, if a recruited participant is known to show an unfavorable outcome, they might be recruited into the control arm or denied participation in the intervention arm. (1-3, 9)
4) Quality of trial:
Maintaining the overall quality of following the trial protocol and data quality/follow up is an important consideration in a logistically challenging cluster trial. (2)
Conclusions
This blog summarizes a basic overview on what a cluster randomized trial is, the basic features and considerations, and the challenges associated with designing and conducting a cluster randomized trial. This blog is just to get you started with the concepts of a cluster randomized trial.




No Comments on Cluster Randomized Trials: Concepts
Excellent presentation.
18th November 2023 at 12:19 pm